The hydrogen economy is becoming a reality! Following Dan Sadler's report to us at the Royal Society Scientific Discussion Meeting: The challenges of hydrogen and metals, on his feasibility study of converting a city's natural gas network to hydrogen; Government has announced the search for the first city in which this will be implemented. Of course a high pressure network using existing steel pipes brings us to the urgency in solving the problem of hydrogen embrittlement of steel. See the recent SINTEF announcement.
A big question in hydrogen embrittlment is whether the dramatic loss in fracture toughness is a consequence of hydrogen induced decohesion across the fracture surfaces, or as a result of enhanced localised plasticity. In the latter case, the issue at hand is whether hydrogen increases or decreases dislocation velocity and what role it plays in the collective action of dislocations to produce localisation.
The kinetic Monte Carlo simulations are all the work of Ivo Katzarov. Dimitar and I just helped a bit with the graphics (and the funding—that's the one thing I'm good at). While modellers at the large length and time scales (such as discrete dislocation dynamics or crystal plasticity finite elements) require constitutive relations including dislocation mobilities as a function of hydrogen concentration and temperature, nothing was available until we undertook to make calculations of dislocation velocity predicated on density functional theory input concerning the energetics of hydrogen trapping at core and kink sites of a dislocation.
Ivo developed a kMC theory that we published in 2017 [1]. There we showed snapshots from kMC simulations and here I show the actual movies that we made. I think that it provides real insight to visualise the actual motion of a dislocation and its trapped hydrogen, even though the situation is stylised as a long straight screw of length 245nm whose ends are terminated by periodic boundary conditions.
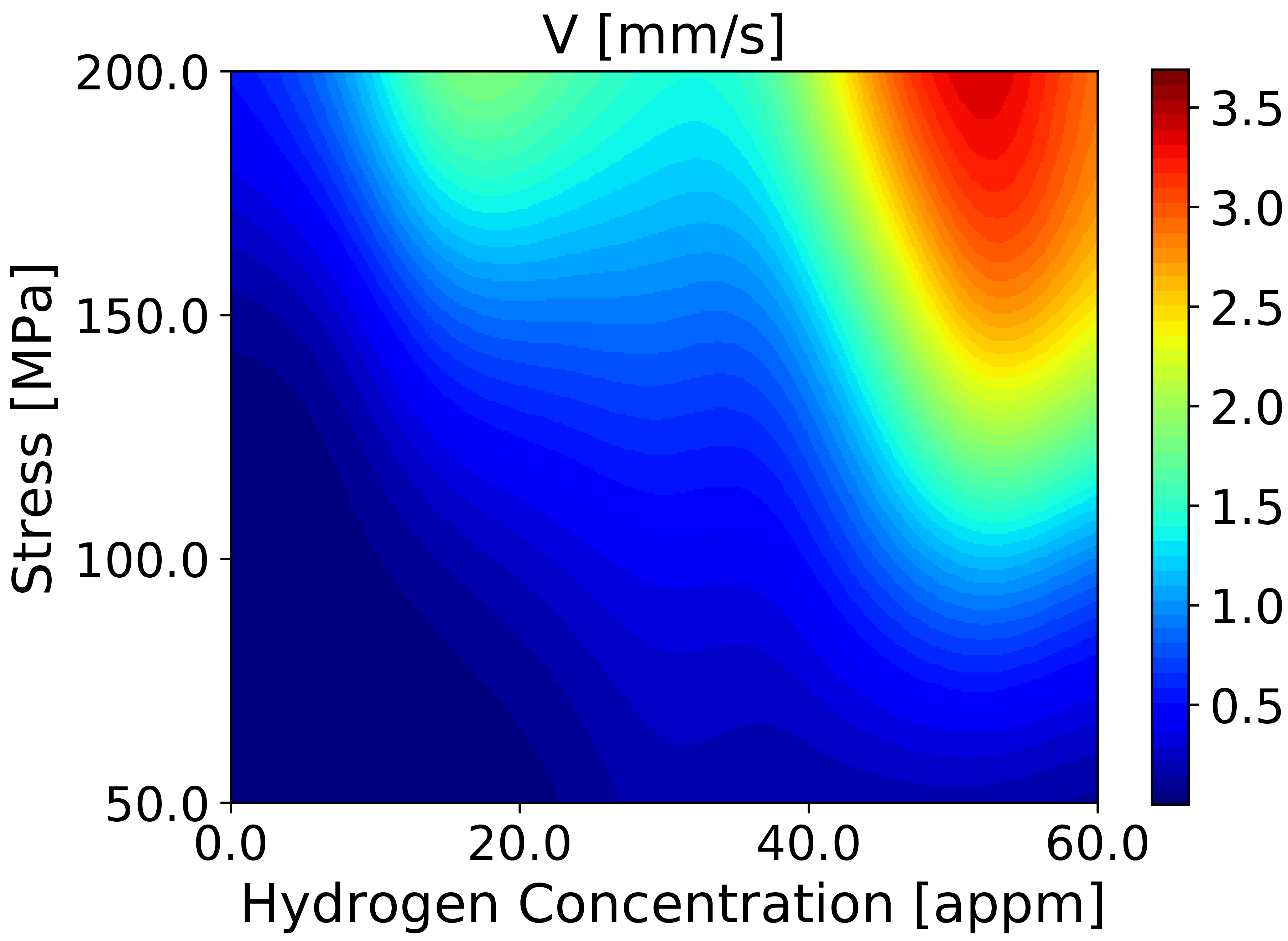
Later Ivo greatly improved the model which is now sufficiently sophisticated that we name it the self consistent kinetic Monte Carlo (SCkMC). This resulted in the figure here, which shows predicted dislocation velocity as a function of stress and hydrogen concentration at room temperature.

You can read a good introductory account of the dislocation dynamics, including the geometry of slip in bcc metals in Omar Al-lahham's MSc thesis. The most important fact to know is that slip in bcc metals, including iron, is thermally activated through the creation of kink pairs and their separation under stress. There are two regimes.
It's important to appreciate that in these videos there is just one dislocation. The upper image is a projection onto the primary glide plane and the lower image is a projection at right angles to this. The amount by which the dislocation deviates in the lower image is a measure of the amount of cross slip. In all the simulations the crystal is oriented for non symmetric triple slip in which the maximum resolved shear stress acts on a plane bisecting the primary glide plane at an angle of 15°.
This is pure iron and so kink pair nucleation is slow on the time scale of kink migration. So you expect no kink collisions and the dislocation will move as a straight object as in fcc metals. However this simulation is at 400K so towards the end you do observe the collision of kinks and the accumulation of prismatic debris, shown in red.
Here at a dissolved H concentration of just 0.5 atomic parts per million, we observe a dramatic change in mechanism of glide. There is significant cross slip indicating the activation of secondary glide planes and considerable accumulation of debris.
Hydrogen atoms (protons) are coloured blue.
Fe, 25 appm H, 300K, 50MPa These are the same conditions as the previous simulation except that the hydrogen concentration is increased to 25 appm. This increases the amount of hydrogen trapped in the dislocation core, which in turn reduces the kink velocity by solute drag and hence increases the likelihood of kink collisions (since the kinks spend more time resident on the dislocation line, the probability of further kink pair formation is increased before the dislocation can become kink-free). Compared to the case of 0.5 appm hydrogen, the debris occurs earlier in the simulation and it is more ubiquitously distributed. There is also more cross slip.
If the stress is greater, then the likelihood of kink pair formation on secondary glide planes is increased and so there are more kink collisions that will cause jogs and in addition more cross slip. On the other hand the kink speed increases with stress and this will have the opposite effect. This illustrates the complex and often competing processes that conspire to effect an average dislocation velocity which is often a compromise of opposing forces.
At higher temperature, even though the hydrogen concentration is higher than in the other examples, its effect is lessened since protons are less strongly trapped due to the thermally activated escape from a trap. Again this simulation reflects the balance between a high stress activating slip on planes less favourably oriented for glide, and the stress increasing the kink velocity. A third factor which enters all of the simulations is the effect of hydrogen on the frequency of kink pair formation—this may be understood from the point of view of Reiner Kirchheim's "defactant".
Last modified: 20 Feb 2021 (Tony Paxton)